Ja, detta med sopskåp var ju klurigare än jag hade trott. Men jag har pratat med lite olika människor om det och tror jag kommit fram till vilken matematik som ska användas. Jag har inte testat detta ännu, så det är än så länge bara teori, men enligt teorin så ska det fungera så här, och jag skriver detta lika mycket för min egen skull som för någon annan som kanske ska göra samma sak.
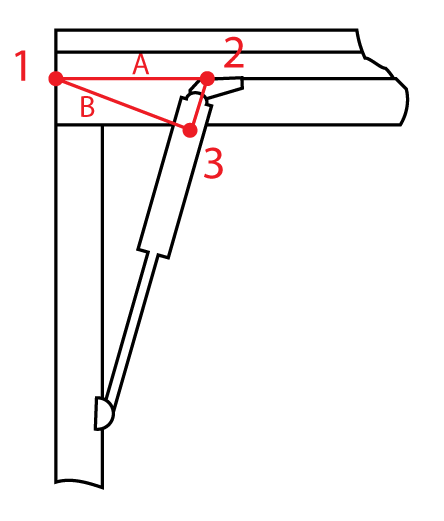
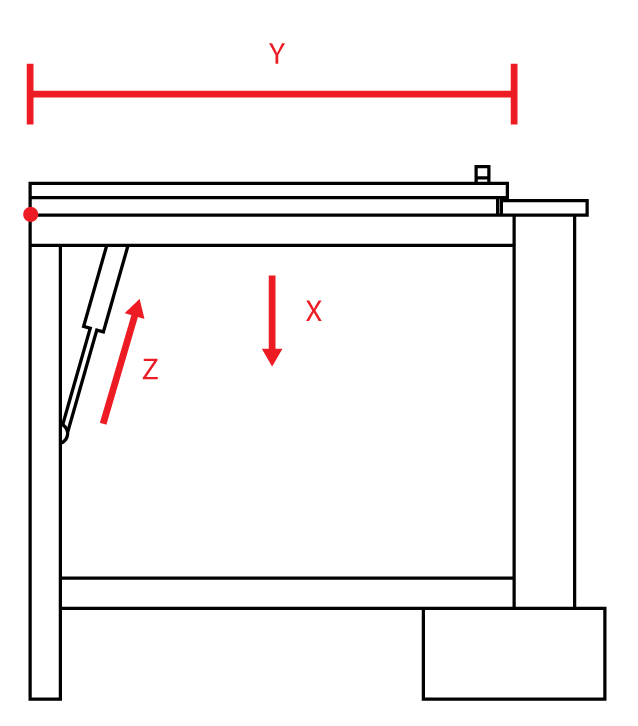
Om man kollar på bilden ovan så ser ni bokstäverna X, Y och Z, samt siffrorna 1, 2 och 3 tillsammans med bokstäverna A och B. Då jag redan har gasfjädrar så vill jag alltså ta reda på längden mellan punkt 1 och 2, det vill säga värdet för A, för att uppnå balans mellan nedåtkraften X och upptåkraften Z så att det är enkelt att öppna luckan.
Detta är ekvationen för att räkna ut den jämnvikten. Den kan se lite skrämmande ut, men den går också att skriva på det här viset: ( ( X * 9,81 ) * ( Y / 2) ) / Z, alltså vikten gånger accelerationen gånger hälften av längden delat med motkraften.
Så dessa är mina värden med andra ord, och resultatet av det blir som ni ser 14,0213. Men detta är inte värdet för A, utan värdet för B, det vill säga hävarmens längd. Nu sitter mina gasfjädrar så att skillnaden mellan dessa två värden förmodligen inte är nämnvärt stora, men man vill ju ändå veta lite mer exakt.
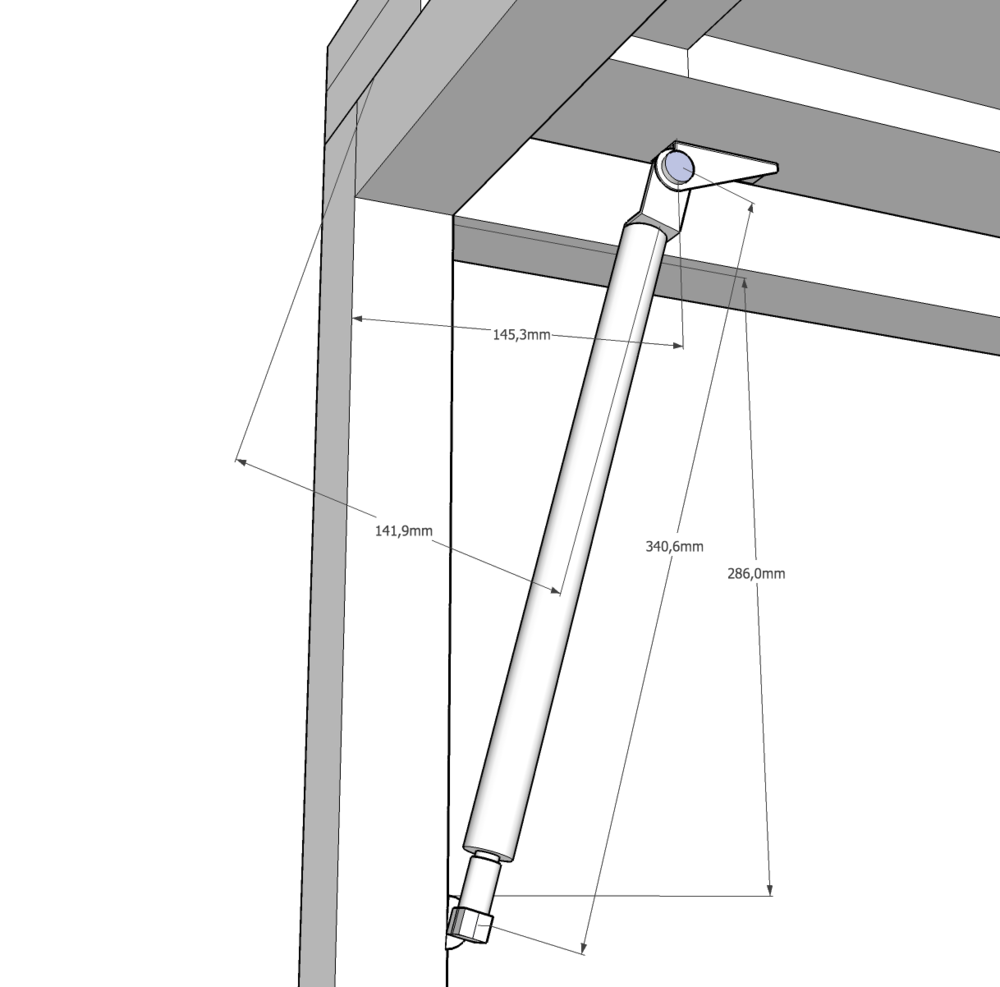
Så då måste vi veta gasfjäderns längd, för att räkna ut de övriga värdena. Mina gasfjädrar är ungefär 34cm långa i ihopstryckt skick, så om man matar in alla dessa siffror så får man något som ser ut som bilden här nedan. Jag har valt att göra det i ett 3D-program för att jag tänkte skriva om det här, men det går ju att kladda på ett millimeterpapper lika gärna.
Så min tanke här är att jag inte vill ha en exakt jämnvikt, utan luckan ska ju helt klart hålla sig stängd när man inte är där och donar. Så det är frågan just hur mycket kraft man behöver. Om vi ökar hävarmens längd till 142mm i stället för de 140 som uträkningen gav oss så får vi alltså ett mått på A som är 145mm, och nedre fästen ska då sitta 286mm ned. Enkelt!
Jag har ännu inte testat detta, men det känns som att jag gjort tillräckligt mycket förarbete för att det ska kunna fungera. Så nu till praktiken! Mer rapport kommer sen!

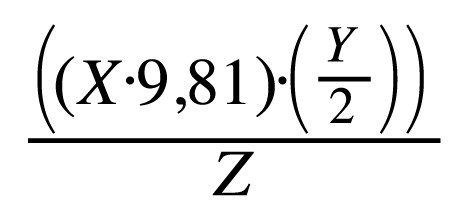
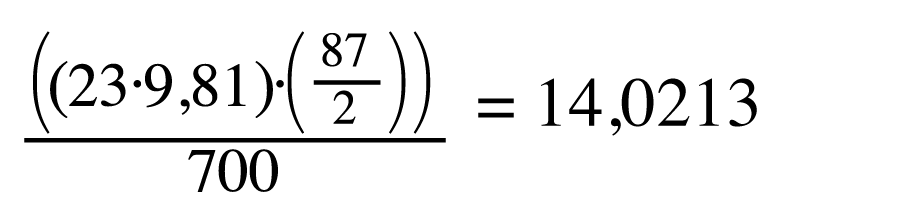
Men antar att det är Kg och cm ?